The efficacy of embeddings in machine learning can be attributed to their ability to transform diverse data types, such as images, text, and audio, into numerical representations. My longstanding interest in linear algebra, encompassing concepts like eigenvalues, eigenvectors, and Jordan form decomposition, predates the emergence of data science as a distinct field.

In the realm of machine learning, where computers inherently operate on binary data, numerical vectors serve as a fundamental bridge between raw data and computational processes. Prior to the mainstream adoption of tools like ChatGPT, the necessity to convert multimodal datasets into numerical vectors was paramount. Consequently, vectors have assumed a foundational role within the machine learning paradigm.

It is imperative to recognize that vectors fundamentally serve as abstractions for various entities, ranging from images to textual documents. They encode essential features and characteristics, enabling the quantitative analysis of inherently diverse data sources.

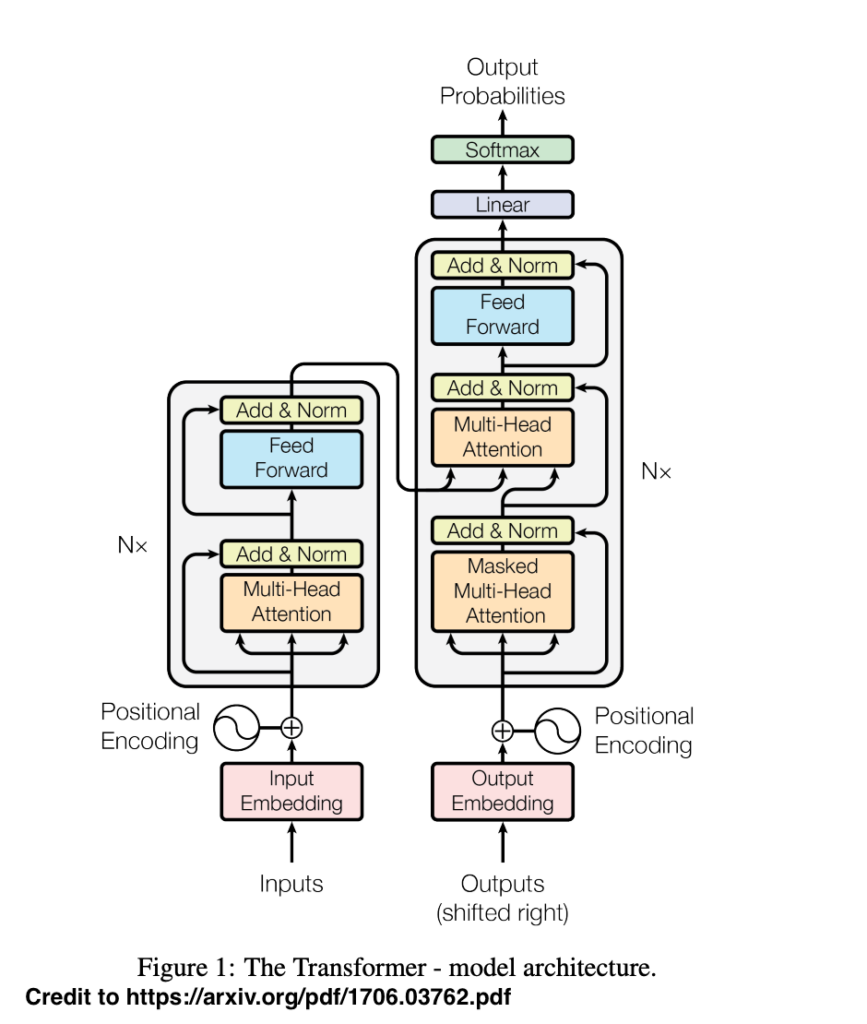
In recent years, an abundance of insightful resources in the form of videos and scholarly papers have shed light on the significant developments within the machine learning domain. However, a pivotal starting point for understanding these advancements often traces back to the seminal paper titled “Attention Is All You Need” (https://arxiv.org/pdf/1706.03762.pdf), which has served as the bedrock for the transformative Transformer model.